功
概念
表述
一个物体受到力的作用,并在力的方向上发生了一段位移,这个力就对物体做了功。功是能量转化的量度。
条件
- 力
- 物体在力的方向上的位移
定义式、单位
- 定义式 W=Fl\cos\alpha
为什么要沿力的切向和法向正交分解?力的合成与分解不是可以选取任意方向吗?
- 单位:焦耳,简称焦,符号为 J
功得表达式也可以写成矢量内积的形式 W=\overrightarrow{F}\cdot\overrightarrow{l}


标矢性
功是标量,但它可以分为正功、负功
功比大小时不看正负号,只看绝对值
变力做功
类动摩擦力
- 特点:力 F 的大小不变,方向与 v 方向夹角恒定
- 方法:W=F'\cdot S,其中 F' 是力 F 沿速度 v 方向的分量大小,S 是路程
类弹簧弹力
- 特点:力的方向不变,大小随位移线性变化
- 方法:W=\frac{F_{1}+F_{2}}{2}\cdot l
F-l 图像的面积表示做功
练习
用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比,即 F_f=kx (其中 x 为铁钉进入木块的深度),在铁锤击打第一次后,铁钉进入木块的深度为 d。求:(1)铁锤对铁钉做功的大小;(2)若铁锤对铁钉每次做功都相等,求击打第二次时,铁钉还能进入的深度。
多个力做功
功是一个过程所对应的量,因此功是过程量
合力做的功等于各个力做功的代数和
- W_\text{合}=F_\text{合}l\cos\alpha(\alpha 为 F_\text{合} 与位移 l 的夹角)
- W_\text{合}=W_1+W_2+W_3+\cdots(即总功为为各个分力所做功的和)
练习
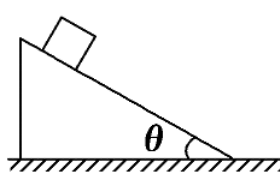
物体沿着倾角为 \theta 粗糙斜面滑倒底端,斜面长度为 s, 求力对物体做的总功。

功率
概念
描述做功快慢的物理量
定义
- 定义:一段时间 t 内力做的功为 W,则功 W 与时间 t 之比叫做功率
- 定义式:P=\frac{W}{t}
单位
瓦特(W)或 J /s
标矢性
标量,一般都是正值
平均功率
\bar{P}=\frac{W}{t}
练习
质量 60 kg 的人,登上大厦的第 11 层用了 3 min,如果该楼每层高 3.0 m, g=10 m/s,则在整个过程中,求这人克服重力做功的平均功率。
上楼问题埋伏的坑:从 1 层到 11 层实际爬了 10 层楼
瞬时功率
P=Fv\cos \theta
\overrightarrow{P}=\overrightarrow{F}\cdot\overrightarrow{v}
\bar{P}=F\bar{v}\cos \theta
练习 1
质量为 m 的小球以初速度 V_0 水平抛出,恰好垂直打在倾角为 \theta 的斜面上(不计空气阻力),计算球落在斜面上时重力的瞬时功率。
练习 2
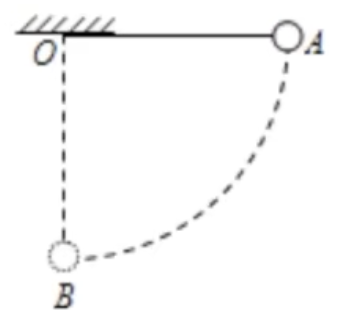
如图所示,长为 L 的细绳一端固定在 O 点,另一端系一质量为 m 的小球。开始时,细绳被拉直并处于水平位置,球处在与 O 点等高的 A 位置。现将球由静止释放,则它从 A 点运动到最低点 B 的过程中,分析重力瞬时功率的变化情况
汽车启动问题
核心方程:
\begin{cases} F-f=ma \\ P=Fv \end{cases}
以恒定功率启动
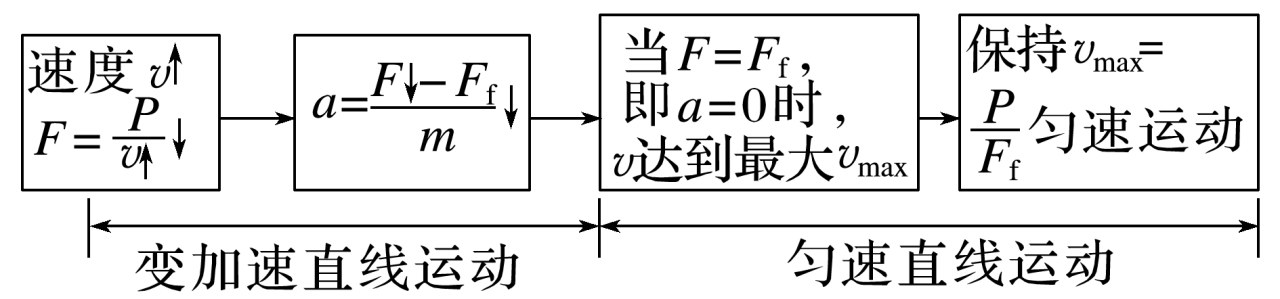
以恒定加速度(牵引力)启动
练习
汽车在平直公路上以速度 v_0 匀速行驶,发动机功率为 P;快进入闹市区时,司机减小了油门,使汽车的功率立即减小一半并保持该功率继续行驶,汽车所受阻力不变。作出汽车从减小油门开始的速度与时间关系图。
练习
一赛车在平直赛道上以恒定功率 200\;kW 加速,受到的阻力不变,加速度 a 和速度 v 的倒数的关系如图所示,求赛车受到的阻力和赛车的质量。
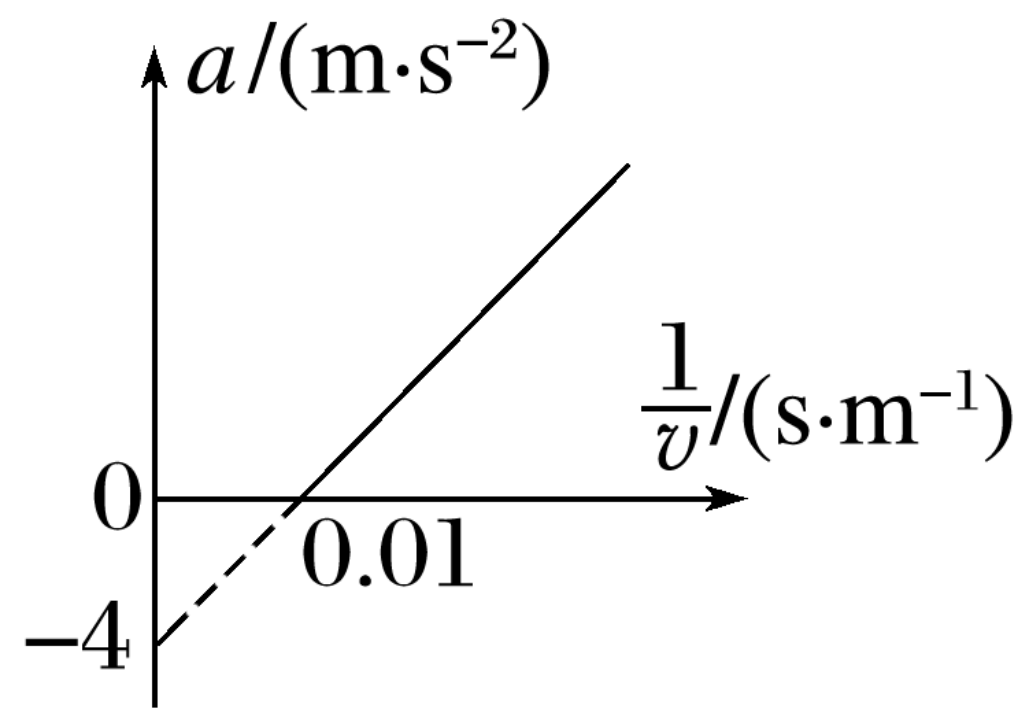
方法 1
- 根据最大速度求出 f
- 找一个特殊点代入,求m
方法 2
\begin{cases} P=Fv \\ F-f=ma \end{cases} \Rightarrow P=(f+ma)v \Rightarrow a=\frac{P}{m}\frac{1}{v}-\frac{f}{m}
练习
一质量为 4.0×10^3\; kg,发动机额定功率为 60 kW 的汽车从静止开始以 a=0.5\;m /s^2 的加速度做匀加速直线运动后以额定功率运动,它在水平面上运动时所受阻力为车重的 0.1 倍,g 取 10\;m / s^2 ,求: 1. 汽车起动后 4 s 末发动机的输出功率; 2. 汽车以 0.5\;m ⁄s^2 的加速度做匀加速运动所能行驶的时间; 3. 汽车在此路面上所能行驶的最大速度; 4. 汽车若以额定功率从静止启动时,当速度达到 6\;m/s 时其加速度大小
(1)
v_{1}=at_{1}=2\,m /s \\ F-kmg=ma\Rightarrow F=m(a+kg)=6\times 10^{3}\,N \\ P_{1}=Fv_{1}=1.2\times 10^{4}\,W
(2)
v_{2}=\frac{P}{F}=10\,m /s \\ t=\frac{v_{2}}{a}=20\,s
(3)
v_{m}=\frac{P}{kmg}=15\,m /s
(4)
F'=\frac{P}{v'}=1\times 10^{4}\,N \\ F'-kmg=ma \Rightarrow a=1.5\,m /s
练习
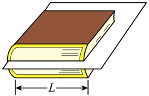
一本现代汉语词典置于水平桌面上,一张 A 4 纸(质量和厚度均可忽略不计) 夹在字典最深处。假设字典的质量分布均匀,同一页纸上的压力分布也均匀,字典总质量 M =1.5\; kg,宽 L=15\; cm,高 H=6\; cm,A 4 纸上下表面与书页之间的动摩擦因数均为 \mu_{1}=0.3,字典与桌面之间的动摩擦因数为 \mu_{2},各接触面的最大静摩擦力近似等于滑动摩擦力,水平向右拉动 A 4 纸,当 A 4 纸夹在字典中离桌面的高度 h=4\; cm 时,字典恰好能被拖动。重力加速度 g 取 10\; m/s^{2},求:
- 字典与桌面之间的动摩擦因数 \mu_{2};
- 若将 A4 纸夹在字典最深处,且离桌面高度为 4.5\;cm,用水平向右的拉力 F 将 A4 纸从字典中匀速抽出,写出拉力 F 与 A4 纸位移 x 的函数表达式(在抽出 A4 纸的过程中,只有与 A4 纸上方重叠部分的字典才对 A4 纸有压力)。
- 上问中将 A4 纸完全拉出字典至少需要做多少功。 (结果保留两位有效数字)
(1)
\begin{cases} f_{1}=\mu_{1}\frac{H-h}{H}Mg=1.5\,N \\ 2f_{1}=\mu_{2}Mg \end{cases} \Rightarrow \mu_{2}=0.2
(2)
F=2\mu_{1}\frac{H-h'}{H}\frac{L-x}{L}Mg=2.25-15x\,(N),\;1\leq x\leq 0.15\,m
(3)
作图,求面积得 W==\frac{9\times 15}{2\times 4}\approx 0.17\,J