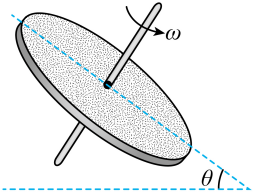
练习 1
如图,半径为 R 的匀质实心圆盘。盘面与水平面的夹角为 \theta,开始时圆盘静止。其上表面均匀覆盖着一层细沙没有掉落,细沙与盘面间的动摩擦因数为 \mu,设最大静摩擦力等于滑动摩擦力。现让圆盘绕垂直于盘面的固定对称轴旋转,其角速度从 0 开始缓慢增加到 \omega(未知)。此时圆盘表面上的细沙有 \frac{8}{9} 被甩掉,重力加速度为 g。则 \omega 的值为
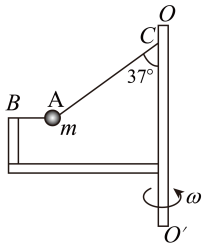
练习 2
如图所示,小球 A 可视为质点,装置静止时轻质细线 AB 水平,轻质细线 AC 与竖直方向的夹角 37°。已知小球的质量为 m,细线 AC 长 l,B 点距 C 点的水平和竖直距离相等。装置能以任意角速度绕竖直轴转动,且小球始终在 BO'O 平面内,那么在角速度 \omega 从零缓慢增大的过程中,分析细线 AC 和 AB 的张力变化情况(求出角速度 \omega 的临界值 )
练习 3
如图所示,厨师在展示厨艺时,将蛋糕放置在一水平托盘上,并控制托盘做竖直平面内半径为 R 的匀速圆周运动,托盘始终保持水平。蛋糕可视为质点,与托盘之间的动摩擦因数为 \mu,最大静摩擦力等于滑动摩擦力,重力加速度为 g。若蛋糕始终与托盘保持相对静止,则托盘做匀速圆周运动的最大速率为

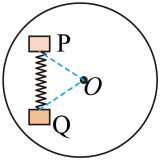
练习 4
如图所示(俯视图),用自然长度为 L_0 劲度系数为 k 的轻质弹簧,将质量均为 m 的两个小物块 P、Q 连接在一起,放置在能绕 O 点在水平面内转动的圆盘上,物体 P、Q 和 O 点恰好组成一个边长为 2 L_0 的正三角形。已知小物块 P、Q 和圆盘间的最大静摩擦力均为,现使圆盘带动两个物体以不同的角速度做匀速圆周运动,求:(1) 圆盘对 Q 的摩擦力的大小等于弹簧弹力的大小时,圆盘的角速度 \omega;(2) 当物块 P、Q 刚要滑动时,圆盘的角速度 \omega;(3) 圆盘对 P 的摩擦力最小时的角速度 \omega。