LovePhysics - 宇宙航行

三个宇宙速度

第一宇宙速度

意义：地球卫星在地面附近绕地球做匀速圆周运动的速度，既是最小发射速度，也是最大环绕速度。
大小：7.9\;\text{km/s}
计算方法：
- G\frac{Mm}{R^{2}}=m\frac{v^{2}}{R}\Rightarrow v=\sqrt{\frac{GM}{R}}
- mg=m\frac{v^{2}}{R}\Rightarrow v=\sqrt{ gR }

例

我国“天问一号”火星探测器成功实现环绕火星运行，并着陆火星。火星的半径是地球的 n 倍，火星的质量为地球的 k 倍，不考虑行星自转的影响，求：(1) 火星表面的重力加速度是地球的几倍？(2) 火星的第一宇宙速度是地球的几倍？

第二宇宙速度

意义：物体挣脱地球引力束缚的最小发射速度
大小：11.2\; \text{km/s}

第三宇宙速度

意义：物体挣脱太阳引力束缚的最小发射速度
大小：16.7\; \text{km/s}

人造地球卫星

近地卫星和同步卫星

近地卫星：r\approx R
地球同步卫星：T = 1\; \text{day}

四个重要物理量

G\frac{Mm}{r^{2}}= \begin{cases} m\frac{v^{2}}{r} & \Rightarrow v=\sqrt{\frac{GM}{r}}\\ m\omega^{2}r & \Rightarrow\omega=\sqrt{\frac{GM}{r^{3}}}\\ m\left(\frac{2\pi}{T}\right)^{2}r & \Rightarrow T=2\pi\sqrt{\frac{r^{3}}{GM}}\\ ma & \Rightarrow a=\frac{GM}{r^{2}} \end{cases}

可见： r 越大，v 、\omega、a_{n} 越小，T 越大。可记为高轨低速大周期

近地轨道与最大环绕速度

轨道半径 r 最小时，线速度 v 最大，飞行器在近地轨道上达到最大环绕速度

例

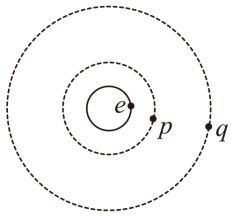
地球赤道上的山丘 e，近地资源卫星 p 和同步通信卫星 q 均在赤道平面上绕地心做匀速圆周运动．设 e、p、q 做圆周运动的速率分别为 v_1、v_2、v_3，向心加速度大小分别为 a_1、a_2、a_3，角速度分别为 \omega_{1}、\omega_{2}、\omega_{3}，周期分别为 T_1、T_2、T_3，写出 e、p、q 的各物理量的大小关系。

注意

口诀“高轨低速大周期”仅适用于“天上的物体”（向心力由万有引力提供）
涉及“地上的物体”，要以同步卫星作为跳板进行比较
完整的口诀：高轨低速大周期，同步卫星看地面

天体的追及相遇

角速度与角度关系：(\omega_{A}\pm\omega_{B})t=\Delta \theta
周期与圈数关系：\frac{t}{T_{A}}\pm\frac{t}{T_{B}}=\Delta n

例

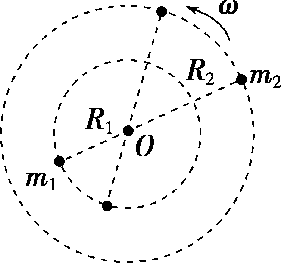
如图，有 A、B 两颗行星绕同一恒星 O 做圆周运动，运行方向相反。A 行星的周期为 T_{A}，B 行星的周期为 T_{B}，在某一时刻两行星相距最近，分别求两行星运动到相距最近和最远所需的时间间隔。

卫星变轨

3D 变轨演示

2D 变轨演示

例

已知地球半径为 R，地球表面的重力加速度为 g_0，飞船在绕地球的圆形轨道Ⅰ上运动，A 点距地球表面的高度为地球半径的 3 倍，飞船到达轨道 \mathrm{I} 的 A 点时点火变轨进入椭圆轨道 \mathrm{II}，到达轨道的近地点 B 时再次点火进入近地轨道 \mathrm{I I I} 绕地球做圆周运动。已知引力常量 G，把地球看做质量分布均匀的球体，求：

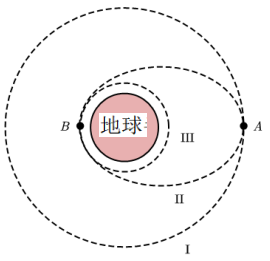
两次点火分别是加速还是减速，向前点火喷射还是向后点火喷射；
飞船在轨道 \mathrm{I} 上的运行速率；
飞船在轨道 \mathrm{I I I} 上绕地运行一周所需的时间；
飞船在轨道 \mathrm{II} 上第一次从 A 到 B 的时间；
若飞船在轨道 \mathrm{I I} 上经过 A 点的速度大小为 v，求在轨道 \mathrm{I I} 上经过 B 点的速度大小；
比较 T_{\mathrm{I}}、T_{\mathrm{I I}}、T_{\mathrm{I I I}} 的大小关系；
比较 v_{\mathrm{I}A}、v_{\mathrm{I I}A}、v_{\mathrm{I I}B}、v_{\mathrm{I I I}B} 的大小关系；
比较 v_{\mathrm{I}A} 与 v_{\mathrm{I I}A}；v_{\mathrm{I I}B} 与 v_{\mathrm{I I I}B} 的大小关系。

双星/多星问题

相等关系

距离不变，F_{n} 相等
同轴转动，\omega,T 相等

易错点

双星系统圆周运动的圆心在双星连线上一点，因此轨道半径 r 不等于双星间的距离 L。

结论

\begin{cases} G\frac{m_{1}m_{2}}{L^{2}}=m_{1}\omega^{2}r_{1} \\ G\frac{m_{1}m_{2}}{L^{2}}=m_{2}\omega^{2}r_{2} \end{cases} \Rightarrow \frac{m_{2}}{m_{1}}=\frac{r_{1}}{r_{2}}

又因为 v=\omega r 和 a=\omega^{2}r，得

\frac{m_{2}}{m_{1}}=\frac{r_{1}}{r_{2}}=\frac{v_{1}}{v_{2}}=\frac{a_{1}}{a_{2}}

例

宇宙中两个相距较近的天体称为“双星”，它们以两者连线上的某一点为圆心做匀速圆周运动，但两者不会因万有引力的作用而吸引到一起。设两者的质量分别为 m_{1} 和 m_{2}，两者相距为 L。求： (1)双星的轨道半径之比； (2)双星的线速度之比； (3)双星的角速度。

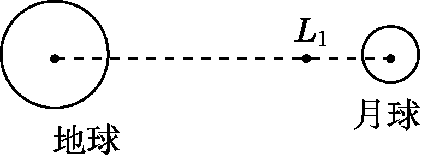
拉格朗日点

定义： 拉格朗日点（Lagrangian point）又称平动点（libration points）在天体力学中是限制性三体问题的五个特殊解（particular solution）

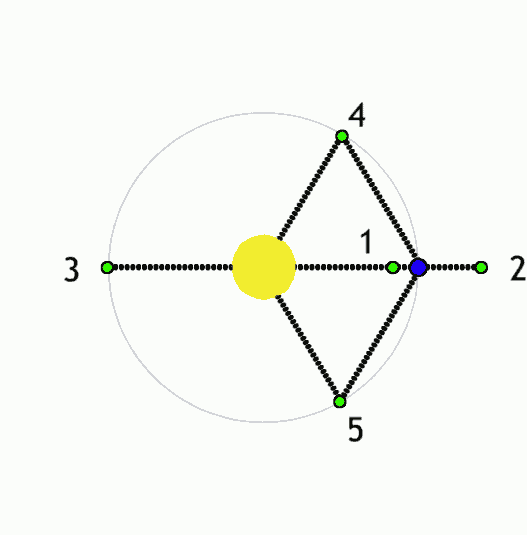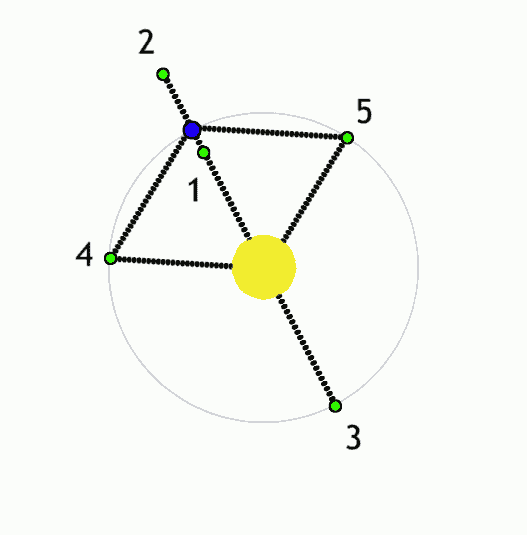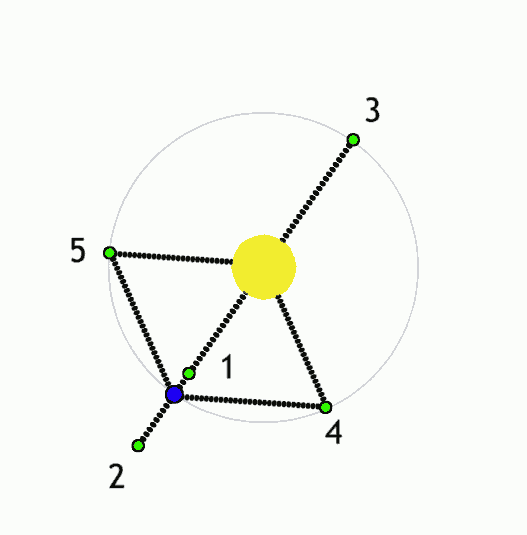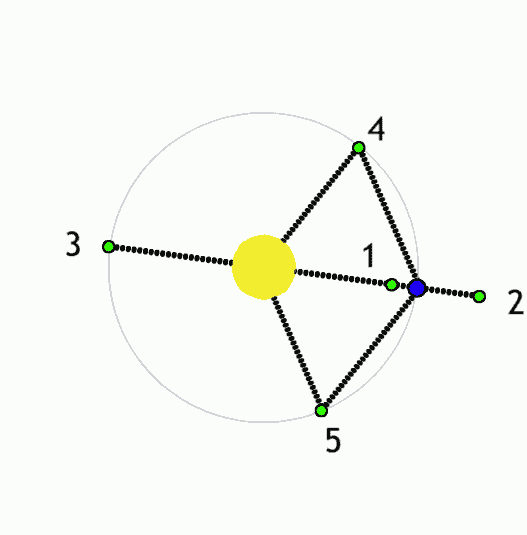
例

如图，拉格朗日点 L_1 位于地球和月球连线上，处在该点的物体在地球和月球引力的共同作用下，可与月球一起以相同的周期绕地球运动。据此，科学家设想在拉格朗日点 L_{1} 建立空间站，使其与月球同周期绕地球运动。以 a_{1}、a_{2} 分别表示该空间站和月球向心加速度的大小，a_{3} 表示地球同步卫星向心加速度的大小。比较 a_{1},a_{2},a_{3} 的大小。