变力做功问题
练习
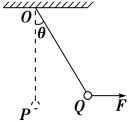
质量为 m 的小球用长为 L 的细线悬挂于 O 点, 小球在水平拉力 E 作用下, 从 O 点的正下方的 P 点移动到 Q 点, 设此时细线与 OP 的夹角为 \theta, 如图所示。在此过程中, 若拉力分别是以下三种情况:
- 用 F 缓慢地拉,求拉力 F 做的功是多少?
- F 为恒力,求拉力 F 做的功?
- 若 F 为恒力, 而且拉到该位置时小球的速度刚好为零,求拉力 F 的大小?
练习
质量为 m 的物体用细绳经过光滑小孔牵引,且在光滑水平面上做匀速圆周运动,拉力为 F 时,转动半径为 R,当拉力逐渐增大到 6F 时,物体仍做匀速圆周运动,此时半径为 R /2,则拉力对物体做功为多大?

解
\begin{cases} m\frac{v_{0}^{2}}{R}=F \\ m\frac{v_{1}^{2}}{\frac{R}{2}}=6F \\ W=\frac{1}{2}mv_{1}^{2}-\frac{1}{2}mv_{0}^{2} \end{cases} \Rightarrow W=6FR-\frac{1}{2}FR=\frac{11}{2}FR
先把等式关系列全,再化简计算,减少不必要的计算步骤
练习
如图所示, 光滑斜面的顶端固定一弹簧, 一质量为 m 的小球向右滑行, 并冲上固定在水平地面上的斜面。设小球在斜面最低点 A 的速度为 v, 压缩弹簧至 C 点时弹簧最短, C 点距地面高度为 h, 重力加速度为 g, 则从 A 到 C 的过程中弹簧弹力做的功是?

解
-mgh-W_{弹}=0-\frac{1}{2}mv^{2}\Rightarrow W_{弹}=\frac{1}{2}mv^{2}-mgh
多过程问题
课本习题
人们有时用“打夯”的方式把松散的地面夯实。设某次打夯符合以下模型:两人同时通过绳子对重物各施加一个力,力的大小均为 F,方向都与竖直方向成 \theta,重物离开地面 h 后人停止施力,最后重物自由下落把地面砸深 l。已知重物的质量为 m。求:
- 重物刚落地时的速度是多大?
- 重物对地面的平均冲击力是多大?

(1)
选取
2F\cos \theta=\frac{1}{2}mv^{2}
(2)
练习
如图所示,AB 与 CD 为两个对称斜面,下部分别与一个光滑的圆弧面的两端相切,圆弧圆心角为 120°,半径 R=2\;m,A 点离圆弧底 M 点的高度为 h =4\;m,现将一个质量 m=1\;kg 的小物块从 A 点静止释放,若小物块与两斜面的动摩擦因数为 0.2,试求:
- 小物块第一次经过圆弧底 M 点时小物块的动能的大小;
- 最终小物块经过圆弧底 M 点时对圆弧的压力的大小;
- 小物块在两斜面上(不包括圆弧部分)一共能走多长路程。(g=10\;m/s^{2})

练习
如图所示,在竖直平面内,长为 L、倾角 \theta=37° 的粗糙斜面 AB 下端与半径 R=1 m 的光滑圆弧轨道 BCDE 平滑相接于 B 点,C 点是轨迹最低点,D 点与圆心 O 等高。现有一质量 m=0.1 kg 的小物体从斜面 AB 上端的 A 点无初速度下滑,恰能到达圆弧轨道的 D 点.若物体与斜面之间的动摩擦因数 \mu=0.25,不计空气阻力,g 取 10 m/s^{2},sin 37°=0.6,cos 37°=0.8,求:
- 斜面 AB 的长度 L;
- 物体第一次通过 C 点时的速度大小 v_{C_{1}};
- 物体经过 C 点时,轨道对它的最小支持力 N_{min};
- 物体在粗糙斜面 AB 上滑行的总路程 s_{总}。

(1)
\begin{cases} h_{AD}=L\sin \theta-R\cos \theta \\ mgh_{AD}-\mu mgL\cos \theta=0 \end{cases} \Rightarrow L=2\,m
(2)
-mgR=0-\frac{1}{2}mv_{C 1}^{2}\Rightarrow v_{C 1}=\sqrt{ 2gR }=2\sqrt{ 5 }\,m /s
从 C 运动到 D。(选取从 D 回落到 C 作为研究时间段也可以)
(3)
\begin{cases} mgR(1-\cos \theta)=\frac{1}{2}mv_{min}^{2} \\ N_{min}-mg=m\frac{v_{min}^{2}}{R} \end{cases} \Rightarrow N_{min}=mg+m\frac{v_{min}^{2}}{R}=1.4\,N
物体最后会在 B 与 B' (B 关于 OC 的对称点) 间往复运动,研究其中一段从 B 到 C 的过程。
(4)
mgL\sin \theta-\mu mg\cos \theta s_{总}=0\Rightarrow s_{总}=\frac{L\tan \theta}{\mu}=6\,m
从 A 点到最后的往复运动(B 点)。
函数最值问题
练习
一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状。此队员从山沟的竖直一侧,以速度 v_{0} 沿水平方向跳向另一侧坡面。如图所示,以沟底的 O 点为原点建立坐标系 Oxy。已知,山沟竖直一侧的高度为 2 h,坡面的抛物线方程为 y=\frac{1}{2h} x^2,探险队员的质量为 m。人视为质点,忽略空气阻力,重力加速度为 g。 1. 求此人落到坡面时的动能; 2. 此人水平跳出的速度为多大时,他落在坡面时的动能最小?动能的最小值为多少?

(1)
\begin{cases} x=v_{0}t \\ y=2h-\frac{1}{2}gt^{2} \end{cases} \Rightarrow y=2h-\frac{g}{2v_{0}^{2}}x^{2}
\begin{cases} y=2h-\frac{g}{2v_{0}^{2}}x^{2} \\ y=\frac{1}{2h}x^{2} \end{cases} \Rightarrow y_{0}=\frac{2h}{1+\frac{gh}{v_{0}^{2}}}
E_{k}-\frac{1}{2}mv_{0}^{2}=mg(2h-y) \Rightarrow E_{k}=\frac{1}{2}m\left( \frac{4g^{2}h^{2}}{v_{0}^{2}+gh}+v_{0}^{2} \right)
(2)
E_{k}=\frac{1}{2}m\left( \frac{4g^{2}h^{2}}{v_{0}^{2}+gh}+v_{0}^{2} \right)=\frac{1}{2}m\left( \frac{4g^{2}h^{2}}{v_{0}^{2}+gh}+v_{0}^{2}+gh-gh \right)\geq \frac{1}{2}m(4gh-gh)
当且仅当 \frac{4g^{2}h^{2}}{v_{0}^{2}+gh}=v_{0}^{2}+gh 即 v_{0}=\sqrt{ gh } 时,E_{k} 取得最小值 \frac{3}{2}mgh