概念回顾
练习
A、B 两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是 4∶3,运动方向改变的角度之比是 3∶2,则它们
A. 线速度大小之比为 4∶3
B. 角速度大小之比为 3∶4
C. 圆周运动的半径之比为 2∶1
D. 向心加速度大小之比为 1∶2
竖直平面内的圆周运动
绳杆模型
非特殊点的受力分析
非特殊位置的竖直圆周运动是指物体在竖直平面内做圆周运动,但不是在最高点或最低点。这类问题通常涉及到向心力、动能、势能、机械能守恒等物理概念。
练习
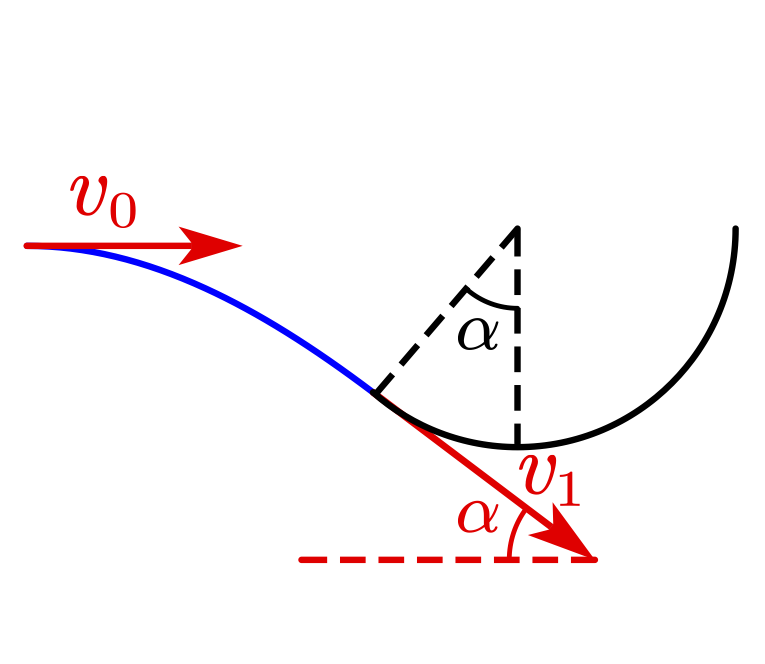
质量为 m 的物体以初速度 v_{0} 从某点水平抛出,恰能沿切线进入半径为 R 的圆弧轨道,已知夹角 \alpha=\frac{\pi}{6},求物体刚进入圆弧轨道时对轨道的压力?
练习
当小球冲上圆轨道的速度 v_{0} 满足 \sqrt{ 2gR }<v_{0}<d\sqrt{ 5gR } 时,会从 P 点脱离轨道,记 P 点与圆心 O 与水平方向的夹角为 \theta,求角度 \theta。(用反三角函数表示)
\begin{cases} \frac{mv^{2}}{R}=mg\sin\theta \\ \frac{1}{2}mv^{2}=\frac{1}{2}mv_{0}^{2}-mg(R+R\sin\theta) \end{cases} \Rightarrow \theta=\arcsin\bigl(\frac{v_0^2-2gR}{3gR}\bigr)
练习
如图所示,一光滑的圆管轨道固定在竖直平面内,质量为 m 的小球在圆管内运动,小球的直径略小于圆管的内径。轨道的半径为 R,小球的直径远小于 R,可以视为质点,重力加速度为 g。现从最高点给小球不同的初速度 v,关于小球的运动,下列说法正确的是
A. 小球运动到最低点时,对外管壁的最小压力为 4mg
B. 小球从静止沿轨道滑落,当滑落高度为时 \frac{R}{3},小球与内、外管壁均没有作用力
C. 小球能再运动回最高点的最小速度 v=\sqrt{ gR }
D. 当 v>\sqrt{ gR } 时,小球在最低点与最高点对轨道的压力大小之差为 5 mg
