练习
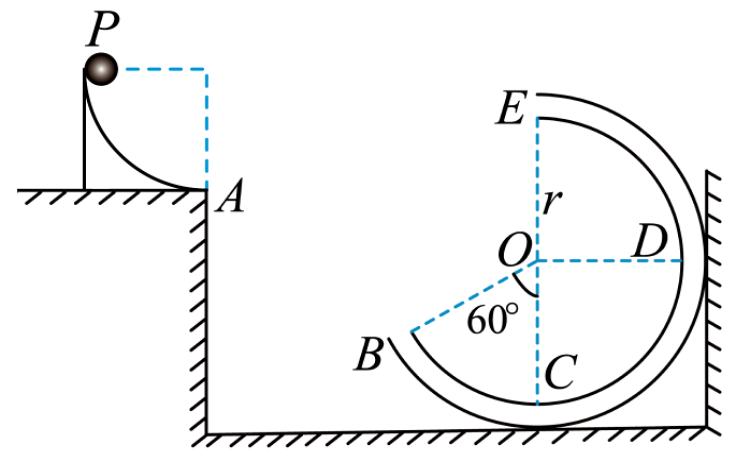
如图所示,水平面上固定放置一四分之一圆弧轨道 PA,轨道的内壁光滑,P 点的切线竖直,A 点在水平面的右边缘且切线水平。在水平面的右下方固定放置一半径为 r 的圆管轨道,D 是轨道上圆心 O 的等高点,EC 是竖直直径,B、E 是管口,管的内壁光滑。
现让质量为 m 的小球(视为质点)从 P 点由静止释放,圆管的内径略大于小球的直径,小球从 A 点离开后,正好从管口 B(与管口无碰撞)进入圆管,然后沿着管壁运动到 E 点,离开 E 点后又刚好落到 B 点。已知 \angle AOC=60^{\circ} ,重力加速度为 g,忽略空气阻力,求:
- 小球在 E 点以及在 B 点的速度大小;
- A、B 两点的高度差;
- 四分之一圆弧轨道 PA 的半径;
- 小球在 D 点时的加速度大小;
- 小球在 C 和 E 点时,对轨道的作用力;
附加思考
如果小球以某一速度 v' 经点 E 进入轨道,小球经过 C、E 对轨道的作用力分别为 F_{C} 和 F_{E},求 F_{E}-F_{C} 与 v' 的关系。
- 小球从 A 点到达 B 点时在 B 点对轨道的作用力;
- 小球从 E 点到达 B 点时在 B 点重力的瞬时功率与小球从 A 点到达 B 点时在 B 点重力的瞬时功率之差。