功能关系

机械能

机械能是对动能和势能的总称，即 E=E_{k}+E_{p}

机械能守恒定律

探究

理想的轻绳下系着一个小球，当小球摆到 A 点的速度为 V_1，高度为 h_1，当它摆到 B 点的速度为 V_2，高度为 h_2，若规定地面的重力势能为零，并忽略一切阻力。用 W_G 表示重力所做的功

1. 试表达重力做功与动能变化的关系；
2. 重力做功和重力势能变化的关系。

概念

1. 内容：在只有重力或弹力做功的物体系统内，动能和势能可以相互转化，而总的机械能保持不变
2. 表达式：
   • E_{k 1}+E_{p 1}=E_{k 2}+E_{p 2}
   • \Delta E_{k}+\Delta E_{p}=0
   • \Delta E_{k}=-\Delta E_{p}

守恒条件

只有物体系统的重力或弹力做功

理解

1. 可以受其他力，但除了重力、弹力，其他力不能做功；

2. 注意研究对象为“系统”。

问题与讨论

判断下列情况的机械能是否守恒？ 1. 竖直上抛运动，平抛运动 2. 物体在光滑的斜面上自由下滑 3. 加速度为 g，竖直向上的匀加速运动 4. 物体在竖直方向合外力为零的运动 5. 小球在弹簧作用下弹出去，忽略一切阻力，试讨论小球在弹射出去过程中它的机械能是否守恒？

研究对象

小球的机械能不守恒，机械能守恒的的研究对象是系统

练习

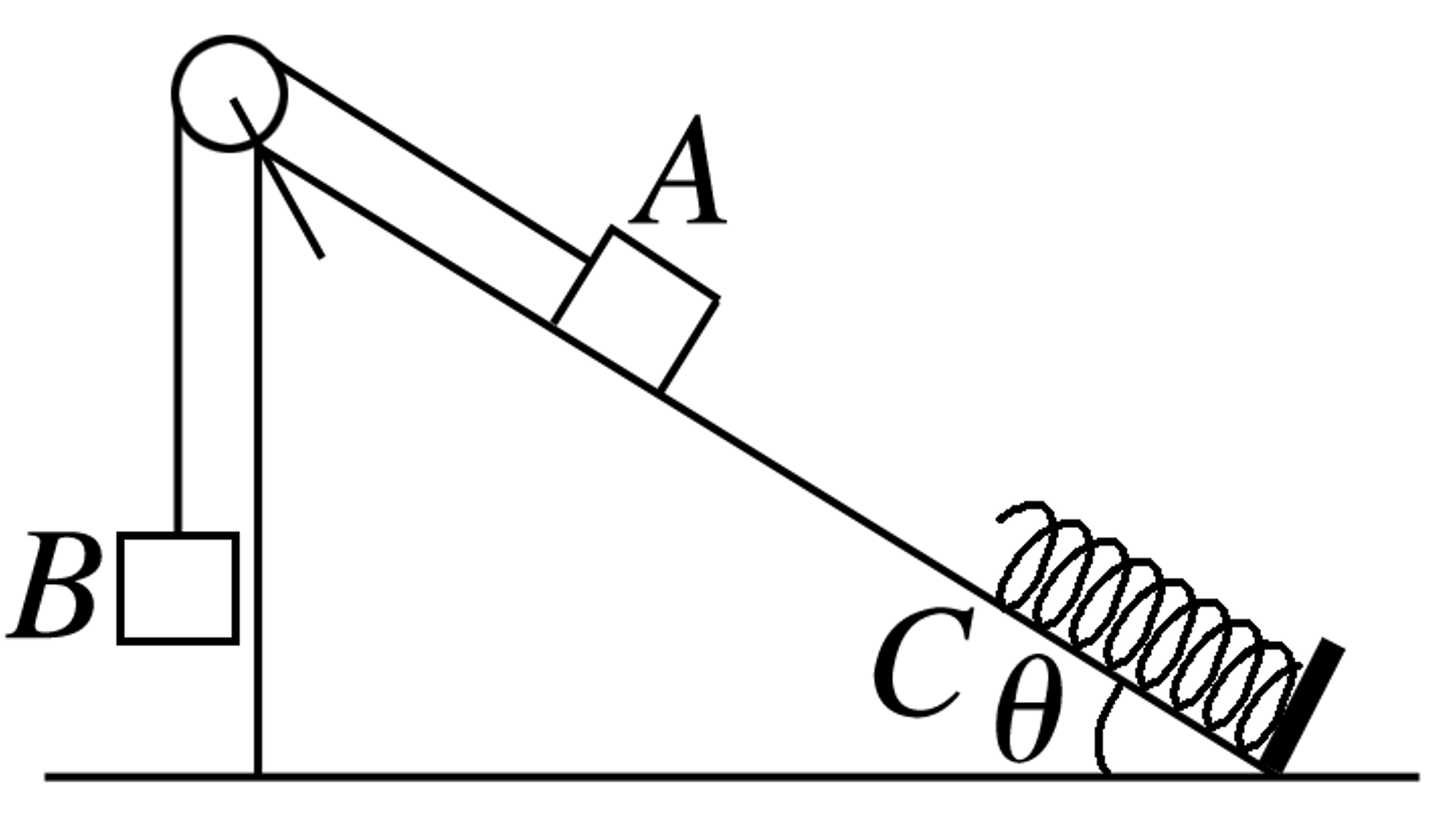
如图所示，固定斜面的倾角 \theta=30^{\circ}，物体 A 与斜面之间的动摩擦因数 \mu=\frac{\sqrt{ 3 }}{4}，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于 C 点，用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体 A 和 B，滑轮右侧绳子与斜面平行，A 的质量为 2m＝4\,kg，B 的质量为 m＝2\,kg，初始时物体 A 到 C 点的距离 L＝1\,m，现给 A、B 一初速度 v_{0}＝3\,m /s，使 A 开始沿斜面向下运动，B 向上运动，物体A将弹簧压缩到最短后又恰好能弹回到 C 点．已知重力加速度 g＝10\,m /s^{2}，不计空气阻力，整个过程中轻绳始终处于伸直状态．求在此过程中：

1. 物体A向下运动刚到C点时的速度大小；
2. 弹簧的最大压缩量；
3. 弹簧的最大弹性势能．