水平圆周运动
圆锥摆
离心/向心运动
例 1
2022年我国航天员在空间站太空舱开设“天宫课堂”,课堂演示了“水油分离”实验。如图所示,用细绳系住装有水和油的瓶子,手持细绳的另一端,使瓶子在竖直平面内做圆周运动,问水油分离后,哪种液体在外侧?(水的密度比油大)
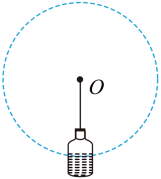
既能用离心运动的知识解释,又能换参考系考虑惯性力分析
圆盘模型
例 1
如图所示,两个质量均为 m 的小木块 a 和 b(可视为质点)放在水平圆盘上,a 与转轴 OO' 的距离为 l,b 与转轴的距离为 2l。木块与圆盘的最大静摩擦力为木块所受重力的 \mu 倍,重力加速度大小为 g,若圆盘从静止开始绕转轴缓慢地加速转动,用 \omega 表示圆盘转动的角速度,求 a 和 b 分别开始滑动的临界速度?

例 2
在上一题的基础上,a 和 b 用长为 l 的水平细绳连接。静止时,绳恰好伸直但无弹力,现让该装置从静止开始转动,使角速度缓慢增大,求:绳上开始有弹力时的角速度;a、b 与圆盘发生相对滑动的角速度。

例 3
在上一题的基础上,将 a 移动到圆盘转轴的另一侧。a,b 的质量分别为 m_{1},m_{2},与转轴的距离分别为 l_{1},l_{2}。求:a,b 在即将相对于圆盘发生滑动时的角速度。

可以运用质点系牛二简化计算
非惯性参考系
质心方程
竖直圆周运动
绳模型
特征:物体在竖直平面内做圆周运动,无支撑

最高点
向心力由重力和拉力提供,重力和拉力方向相同
T + mg = m\frac{v^2}{r}
最高点最小速度(恰好能做圆周运动 or 恰好能过最高点)在绳上的拉力为零时取到
mg = m\frac{v^2}{r} \Rightarrow v = \sqrt{gr}
最低点
向心力由重力和拉力提供,重力和拉力方向相反
T - mg = m\frac{v^2}{r}
杆模型
特征:物体在竖直平面内做圆周运动,有支撑

例题
如图所示,长 L=0.5m 的轻杆一端在 O 点,另一端连接着一个零件 A,A 的质量 m=2 kg,重力加速度 g 取 10 m / s^{2}.现让 A 在竖直平面内绕 O 点做匀速圆周运动,在 A 通过最高点时,求下列两种情况下 A 对杆的作用力: (1) A 的速率为 1\;m / s; (2) A 的速率为 4\;m / s。

详解:
求通过最高点时向心力仅由重力提供的临界速度 v_{0}
mg = m \frac{v_{0}^{2}}{L} \Rightarrow v_{0} = \sqrt{ gL } = \sqrt{ 5 }\; m / s
比较得 v_{1}<v_{0}<v_{2},所以对于 v_{1},杆对其有向上的支持力 F_{N};所以对于 v_{2},杆对其有向下的拉力 F_{T}。
(1)\; mg-F_{N} = m\frac{v_{1}^{2}}{L} \Rightarrow F_{N}=16\; N
(2)\; mg+F_{T} = m\frac{v_{1}^{2}}{L} \Rightarrow F_{T}=44\; N


由于力的作用是相互的, A 对杆的作用力在数值上与 F_{N},F_{T} 相等。
可以不用讨论杆对物体力 F 的方向,假设一个方向列示计算,如果计算结果为证,则 F 与假设的方向相同,否则相反。
向心力是效果力,是根据力的作用效果命名的,没有施力物体。受力分析只需考虑性质力。
