| 公式 | 物理含义 | 适用范围 |
|---|---|---|
| E=\frac{F}{q} | 场强的定义式 | 一切电场 |
| E=k\frac{Q}{r^{2}} | 真空中点电荷场强的决定式 | 真空中,场源电荷 Q 是点电荷 |
| E=\frac{U}{d} | 匀强电场中场强的决定式 | 匀强电场 |
练习
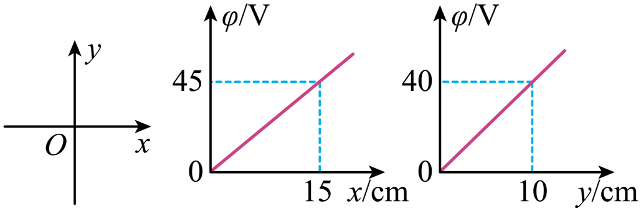
空间存在着平行纸面的匀强电场,但电场的具体方向未知,现在纸面内建立直角坐标系 xOy,用仪器沿 Ox、Oy 两个方向探测该静电场中各点电势,得到各点电势 \varphi 与横、纵坐标的函数关系如图所示。求该电场的电场强度 E。
在匀强电场中沿同一方向任意相等距离上的电势差相等
- 匀强电场中,两条平行线段上相等距离的两点间的电势差相等
\begin{cases} AB / / CD \\ AB = CD \end{cases} \Rightarrow U_{AB} = U_{CD}
- 匀强电场中,任意线段的几何等分点也是电势差等分点
练习
a、b、c、d 是匀强电场中的四个点,它们正好是一个矩形的四个顶点.电场线与矩形所在的平面平行.已知 a 点的电势是 20\;V,b 点的电势是 24\;V,d 点的电势是 4\;V,求 c 点的电势。

练习
如图所示的平面内有 A、B、C、D、E 五点,其中 AC 平行于 DE,B 点为 AC 的中点,AB=DE,平面内存在匀强电场,电场方向与该平面平行,A 的电势 \varphi_{A}=10\;V,C 的电势 \varphi_{C}=4\;V,E 的电势 \varphi_{E}=13\;V,电子的电量为 e。
分别求 \varphi_{B} ,\varphi_{D} ,将电子从_B_点移到_D_点电场力做的功 W_{BD}。

练习
有一匀强电场的方向平行于 xOy 平面,平面内 a、b、c、d 四点的位置如图所示,cd、cb 分别垂直于 x 轴、y 轴,其中 a、O、b 三点电势分别为:4\;V、6\;V、8\;V,一电荷量为 q=-2\times 10^{-5}\;C 的负点电荷由 a 点开始沿 abcd 路线运动。
求:\varphi_{d},场强的大小和方向。

练习
一匀强电场的方向平行于 xOy 平面,平面内 a、b、c 三点的位置如图所示,三点的电势分别为 10\;V、17\;V、26\;V。求:电场强度的大小。

找到两个等势点,构造等势面。
不通过找等势面的方法如何求电场的大小和方向?
多个场源电荷的情况下的电势
多场源的静电场中一点的电势等于每一场源单独存在时在该点的电势的代数和
练习
如图所示,ABC 为等边三角形,电荷量为 +q 的点电荷固定在 A 点。先将一电荷量也为 +q 的点电荷 Q_{1} 从无穷远处 (电势为 0) 移到 C 点,此过程中静电力做功为 -W。再将 Q_{1} 从 C 点沿 CB 移到 B 点并固定。最后将一电荷量为 -4 q 的点电荷 Q_{2} 从无穷远处移到 C 点。求:
- Q_{1} 移入之前,C 点的电势;
- Q_{1} 从 C 点移到 B 点的过程中,所受静电力做的功;
- Q_{2} 在移到 C 点后的电势能。

电场中的图像
\varphi-x 图像
问题
空间有一个沿着 x 轴方向的电场,其 \varphi 随 x 关系如图
- 画出 0\sim x_{2} 区间的电场方向。
- x=x_{1}的电场强度为多少?
- 0 \sim x_{2} 区间,E的大小在怎么变化?
- \varphi - x 为直线,则是什么电场? 斜率表示什么

如果场强 E 平行 x 轴,则 \varphi-x 图像的斜率就是 E
如果场强 E 不平行 x 轴,则 \varphi-x 图像的斜率有什么含义?
E_p-x 图像斜率表示什么?
练习
同一平面内的三点 A、B、C,其连线 AB=d,BC=2d,AB 垂直 BC,匀强电场的电场线与三点在同一平面内。一电子(电量为 -e)从 A 运动到 B,动能将减少 W;一质子(氢原子核,带正电,电量为 +e)从B运动到C,动能将增加2W,求匀强电场的场强。
E-x 图像
图线与x轴围成的“面积”是什么?
电势差
练习
静电场方向平行于 x 轴,其电势 \varphi 随 x 的分布可简化为如图所示的折线,图中 \varphi_{0} 和 d 为已知量。一个带负电的粒子在电场中以 x=0 为中心,沿 x 轴方向做周期性运动。已知该粒子质量为 m、电荷量为 -q,其动能与电势能之和为 -A (0<A<q\varphi_{0})。忽略重力。求:
- 粒子所受电场力的大小;
- 粒子的运动区间;
- 粒子的运动周期。

(1)
E = \frac{\varphi_{0}}{d},\,F = qE = \frac{q\varphi_{0}}{d}
(2)
动能为零时的电势记为 \varphi'
-A = -q\varphi'\Rightarrow \varphi' = \frac{A}{q}
此时,粒子与原点的距离 d' 满足
Ed'=\varphi_{0}-\varphi'\Rightarrow d' = \frac{\varphi_{0}-\frac{A}{q}}{\frac{\varphi_{0}}{d}}= d(1-\frac{A}{q\varphi_{0}})
运动区间为 -d' 到 d'
(3)
粒子的运动周期记为 T,粒子从距
\begin{cases} a = \frac{F}{m} = \frac{q\varphi_{0}}{md} \\ \frac{1}{2}a\left( \frac{T}{4} \right)^{2} = d' \end{cases} \Rightarrow T = 4\sqrt{ \frac{2md^{2}}{q\varphi_{0}}\left( 1-\frac{A}{q\varphi_{0}} \right) }
练习
半径为 R,均匀带正电荷的球体在空间产生球对称的电场;场强大小沿半径分布如图所示,图中 E_{0} 已知,E-r 曲线下 O\sim R 部分的面积等于 R\sim 2R 部分的面积。
- 写出 E-r 曲线下面积的单位;
- 己知带电球在 r\geq R 处的场强 E=k\frac{Q}{r^{2}},式中 k 为静电力常量,该均匀带电球所带的电荷量 Q 为多大?
- 求球心与球表面间的电压 U;
- 质量为 m,电荷量为 q 的负电荷在球面处需具有多大的速度可以刚好运动到 2R 处?

(1)
单位是伏特
(2)
k\frac{Q}{R^{2}} = E_{0}\Rightarrow Q = \frac{E_{0}R^{2}}{k}
(3)
U = \frac{E_{0}R}{2}
(4)
由于两部分面积相等,R\sim 2R 的电势差与 0\sim R 的电势差相等,即为 U = \frac{E_{0}R}{2}
-qU = 0-\frac{1}{2}mv^{2}\Rightarrow v = \sqrt{ \frac{qE_{0}R}{m} }